Topics

• "History teaches the continuity of the development of science. We know that every age has its own problems, which the following age either solves or casts aside as profitless and replaces by new ones. If we would obtain an idea of the probable development of mathematical knowledge in the immediate future, we must let the unsettled questions pass before our minds and look over the problems which the science of today sets and whose solution we expect from the future. To such a review of problems the present day, lying at the meeting of the centuries, seems to me well adapted. For the close of a great epoch not only invites us to look back into the past but also directs our thoughts to the unknown future.

  I should say first of all, this: that it shall be possible to establish the correctness of the solution by means of a finite number of steps based upon a finite number of hypotheses which are implied in the statement of the problem and which must always be exactly formulated. This requirement of logical deduction by means of a finite number of processes is simply the requirement of rigor in reasoning. Indeed the requirement of rigor, which has become proverbial in mathematics, corresponds to a universal philosophical necessity of our understanding; and, on the other hand, only by satisfying this requirement do the thought content and the suggestiveness of the problem attain their full effect.

  I think that wherever, from the side of the theory of knowledge or in geometry, or from the theories of natural or physical science, mathematical ideas come up, the problem arises for mathematical science to investigate the principles underlying these ideas and so to establish them upon a simple and complete system of axioms, that the exactness of the new ideas and their applicability to deduction shall be in no respect inferior to those of the old arithmetical concepts.

  Is this axiom of the solvability of every problem a peculiarity characteristic of mathematical thought alone, or is it possibly a general law inherent in the nature of the mind, that all questions which it asks must be answerable?"
                                                                               David Hilbert

• On Wednesday, August 8, 1900, in Paris, before the International Congress of Mathematicians, David Hilbert (1862-1943) delivered a lecture, modestly entitled   Mathematical Problems, which proved crucial in the development of the modern computer.
  If you read carefully the epigraph above (extracted from the introduction to his lecture), you can see that Hilbert essentially asks the following three questions (see also Jeffrey Shallit's A Very Brief History of Computer Science):
  1. Is mathematics complete?  (can every mathematical statement be either proved or disproved?)
  2. Is mathematics consistent?  (is it true that statements such as 0 = 1 cannot be proved by valid methods?)
  3. Is mathematics decidable?  (is there a 'mechanical' method that can be applied to any mathematical assertion so that—at least in principle—we can know whether that assertion is true or not? this last question became known as the Entscheidungsproblem i.e. the 'decision problem')
  Although Hilbert did not have computers explictly in mind, in retrospect his questions imply not only computers, but a computational view of knowledge and of the world (or at least, the world of science). As All Schombert puts it in his beautiful 21st Century Science, Lecture 8,

  "The technological revolution of the [late 1800's and] early 1900's led some scientists to believe that Nature was basically a computational process. An extension of the clockwork Universe idea, this philosophy regards the entire Universe as a gigantic information-processing system or a cosmic computer. The laws of Nature serve as the programming, the initial conditions at the origin of the Universe are the input, and events of the world are the output."

  Hilbert's questions are very hard, and it took some years before answers started to appear. An important first step was the publication, between 1910 and 1913, by Bertrand Russell (1872 - 1970) and Alfred North Whitehead (1861 - 1947), of the monumental Principia Mathematica, an "attempt to put the whole of mathematics on a logical foundation." The first important breakthrough happened in 1931, when  Kurt Gödel  (1906-1978) showed that every sufficiently powerful formal system (e.g. arithmetic or Euclidean geometry) is either inconsistent or incomplete, and that, if an axiom system is consistent, this consistency cannot be proved within the system itself. This was a remarkable, and rather unexpected, result. It showed that not all questions we ask are answerable—at least within a given framework of assumptions and rules of reasoning. I don' believe it is exaggerated to say that Gödel discovery is comparable to Galileo's discovery that the Earth is not at the center of the universe, or Hubble's discovery that the Milky Way is just one of billions of galaxies in the universe.
  In his article 50 Years Later, The Questions Remain, Peter Suber writes:

  "The first incompleteness theorem showed that some perfectly well-formed arithmetical statements could never be proved true or false. Worse, it showed that some arithmetical truths could never be proved true. More precisely, for every axiomatic system designed to capture arithmetic, there will be arithmetic truths which cannot be derived from its axioms, even if we supplement the original set of axioms with an infinity of additional axioms. This shattered the assumption that every mathematical truth could eventually be proved true, and every falsehood disproved, if only enough time and ingenuity were spent on them.

  The second incompleteness theorem showed that axiomatic systems of arithmetic could only be proved consistent by other systems. This made the proof conditional on the consistency of the second system, which in turn could only be validated by a third, and so on. No consistency proof for arithmetic could be final, which meant that our confidence in arithmetic could never be perfect.

  In quick succession, Gödel deprived arithmetic of its hope of completeness and its certainty of consistency. These were devastating blows to the concepts of logic and mathematics that prevailed in 1931 when Gödel published his proofs at age 25. But the conviction that genius and time could conquer every conjecture and hypothesis, not only in arithmetic, but in all of mathematics generally, had prevailed for the two or three millenia of mathematical history before Gödel's theorems. For this reason Gödel truly seemed to overturn the glory of this glorious subject and bring an epoch to a close. With time, however, mathematicians have adapted to the post-Gödelian world, and many now find mathematics to be more beautiful incomplete than it could ever have been when considered completeable."

• In 1936,  Alan Mathison Turing  (1912-1954), and independently Alonzo Church  (1903-1995), provided a solution to Hilbert's Entscheidungsproblem, the third problem, by constructing a formal model of a universal computer, now known as the Turing Machine, and showing that there were problems such a machine can not solve. You can take a look at Turing's historic paper On Computable Numbers, With an Application to the Entscheidungsproblem. In Turing's words, "the 'computable' numbers may be described briefly as the real numbers whose expressions as a decimal are calculable by finite means." Turing's paper contained three fundamental results:
  1. He shows how to define and formally construct a universal computing machine—the Turing Machine
  2. He shows that there are certain definable numbers which can not be computed by such a machine
  3. He shows that there can not be a 'mechanical' method that can be applied to certain mathematical assertions so that we can know whether such assertions are true or not; this is the answer to Hilbert's Entscheidungsproblem
  With regard to the third item above, Turing proves that "there can be no general process for determining whether a given formula U of the functional calculus Z is provable, i.e. that there can be no machine which, supplied with any one U of these formulae, will eventually say whether U is provable."

   

  

   

   

  

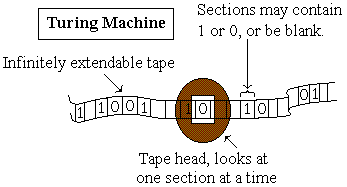
  The Turing Machine

   

• While the negative answer to Hilbert's Entscheidungsproblem dashed our hopes that, at least in mathematics, all questions might be answerable, Turing's formal construction of a universal computer proved pivotal in the development of the modern computer.
  What is a Turing Machine? Here is a brief definition:

  "A Turing machine is a very simple machine, but, logically speaking, has all the power of any digital computer. It may be described as follows: A Turing machine processes an infinite tape. This tape is divided into squares, any square of which may contain a symbol from a finite alphabet, with the restriction that there can be only finitely many non-blank squares on the tape. At any time, the Turing machine has a read/write head positioned at some square on the tape. Furthermore, at any time, the Turing machine is in any one of a finite number of internal states. The Turing machine is further specified by a set of instructions of the following form:

  (current_state, current_symbol, new_state, new_symbol, left/right)

  This instruction means that if the Turing machine is now in current_state, and the symbol under the read/write head is current_symbol, change its internal state to new_state, replace the symbol on the tape at its current position by new_symbol, and move the read/write head one square in the given direction (left or right). If a Turing machine is in a condition for which it has no instruction, it halts.

  Nowadays it is natural to think of the set of instructions as a program for the Turing machine."

  [ from Turing Machines ]

  Notice finally that Turing was able to prove that, under certain fairly general assumptions, certain Turing machines are universal, in the sense that they can simulate any other Turing machine. Modern computers are actual implementations of Universal Turing machines.
• Although the Turing Machine is an abstract formalism, and today is essentially the 'principle' behind our computers, it is also capable of direct implementation, as shown, for example, by Ehud Shapiro's construction of a "mechanical device [which] embodies the theoretical Turing machine." [ see Computing Device To Serve As Basis For Biological Computer ]

  . "Shapiro's mechanical computer has been built to resemble the biomolecular machines of the living cell, such as ribosomes. Ultimately, this computer may serve as a model in constructing a programmable computer of subcellular size, that may be able to operate in the human body and interact with the body's biochemical environment, thus having far-reaching biological and pharmaceutical applications."

• A very interesting application of the Turing Machine was conceived by John von Neumann (1903 - 1957). von Neumann introduced the notion of 'cellular automaton,' a mathematical construct that is essentially a special case of a Turing Machine, but generally not of a 'universal' Turing machine. Among other things, he was interested in constructing, at least on paper, a cellular automaton (which he called a universal constructor which could reproduce or self-replicate. Notice that the fundamental difficulty lies in constructing a new machine which will in turn be able to replicate itself.
  Here is the basic idea: the full automaton consists of 1) a Universal Turing Machine, on whose tape is stored the information required to build the automaton itself; 2) a constructor, which directs the operations of a 3) construction arm, which assembles the copy; 4) a large number of copies of the individual elements of the automaton itself, randomly floating in the environment of the automaton.
  The idea works—on paper. The fact is that the complete automaton consists of some 200,000 cells and 29 states! This is indeed a very tall order, even for a modern computer's simulation, let alone for its physical realization. With regard to simulations, subsequent work by others has reduced these numbers considerably, and simulations are now possible. See, for example, John von Neumann and Cellular Automata or Simulateur de l'Automate de von Neumann en Langage JAVA.

 
Readings, Resources and Questions

• A very good, in depth introduction to the topics discussed in this lecture is Martin Davis, Engines of Logic. Mathematicians and the Origin of the Computer. W W Norton, NY 2000. This work was first published under the title The Universal Computer. The Road from Leibniz to Turing. W W Norton, NY 2000.
• For a reasonably simple exposition of Gödel's work see Ernest Nagel & James R Newman, Gödel's Proof, New York U Press, 1958, or Michael A Arbib, Brains, Machines, and Mathematics, 2nd ed., Springer-Verlag 1987.
• The resources concerning Alan Turing are rightfully quite extensive. In addition to what is in the York's Libraries, here is a short, selected list of websites:
  • Digidome Computer Museum
  • Alan Turing
  • The Alan Turing Home Page
  • The Turing Archive for the History of Computing
  And here is a book and a few websites where you can learn more about, and even play with, Turing Machines:
  • Jon Agar, Turing and the Universal Machine: The Making of the Modern Computer. Totem Books, 2002.
  • Turing Machine Simulator
  • Turing Machines
  • Turing Machine Applet
  • Game: Turing Machine
  Finally, here are two interesting articles on the Turing Machine theme:
  • The Web as a Turing Machine
  • The Biggest Numbers in the Universe